문제인식
N개의 정수들이 있을 때, a번째 정수부터 b번째 정수까지의 합을 구하는 것은 어려운 일이 아니다.
예를 들면, 아래 배열에서 5번째에서 11번째 까지 더하는 방법은 그냥 배열을 돌면서 더하면 된다. 그 시간 복잡도는 대략 O(N) 이다.

하지만 이와 같은 a, b의 쌍이 M개 주어졌을 때는 O(M*N) 이 된다.
너무 오래 걸리니까 더 좋은 방법을 찾아보자.
구간 합을 구할 때마다 N을 전부 도는게 너무 오래 걸린다면,
특정 구간의 합을 미리 저장하고 이 값들의 합을 구해보자.
이때, 이진 트리를 활용할 수 있다.
트리 생성
구간 합을 저장해 보자.

이 전체 의 합은 66이다.
이 구간의 전체의 합은 0 ~ 5 사이의 값의 합(30)과 6 ~ 11 사이의 값의 합(36)으로 둘로 나눠, 이의 합으로 나타낼 수 있다.

- 0 ~ 5 는 0 ~ 2 합 (13)과 3 ~ 5 합 (17)으로 둘로 나뉜다.

- 0~2 는 0~1 의 합 (10) 과 2 의 합(3) 으로 둘로 나뉜다.

- 0~1 은 0 의 합 (1) 과 1의 합 (9)로 둘로 나뉜다.

이 과정을 모든 부분에 대해 진행하면 다음과 같이 나타낼 수 있다.

그 내부의 값은 다음과 같이 저장된다.

이때, 항상 반으로 나누기 때문에 이진 트리의 조건을 만족한다.
이진 트리의 경우 트리 구조를 클래스를 활용하여 생성하지 않고, 일차원 배열로 인덱싱 할 수 있다.
- tree의 시작 index을 1로 잡는다.
- 항상 왼쪽 자식노드는 자신의 인덱스의 2배, 오른쪽 자식노드는 자신의 인덱스의 2배+1 이다.
- 따라서 빈 인덱스가 있을 수도 있다. (18, 19, 22, 23 … 등)
- 또한, 합의 저장하기 때문에 실제 인덱스보다 큰 2의 제곱 수의 2배의 인덱스가 필요하다.
- 포화 이진 트리를 기준으로 리프 노드가 n개 라면 그 위의 노드의 개수는 n-1 개이기 때문

ex) 12개의 요소가 있다면 최소 16개의 2배에 해당하는 32개의 인덱스가 필요하다.
이는 약 4배로 환산할 수 있다.
ex) 12*4 = 48
이를 위한 소스 코드
tree[] = new long[n*4] => tree 구조에 대응되는 1차원 배열
num[] => 입력 배열
/*
* start : 탐색 배열의 범위 시작점
* end : 탐색 배열의 범위 종료점
* index : 현재 채울 tree 의 index
*/
long makeTree(int start, int end, int index) {
//리프노드에 도달하면 더이상 나눌 수 없음 tree 에 입력 후 리턴
if(start == end) return tree[index] = num[start];
//반으로 나눔
int mid = (start+end)/2;
//둘로 나눈 값의 합을 저장하고 리턴
return tree[index] = makeTree(start, mid, index*2) + makeTree(mid+1, end, index*2+1);
}구간 합
이제, 이 트리를 이용하여 구간합을 구해보자.
ex) 5 ~ 11 사이의 값들의 합을 구해보자.

먼저, 내가 확인하고자 하는 범위를 확인한다.
- 아래의 그래프에서 5와 6 ~ 11 의 값을 더하면 된다.
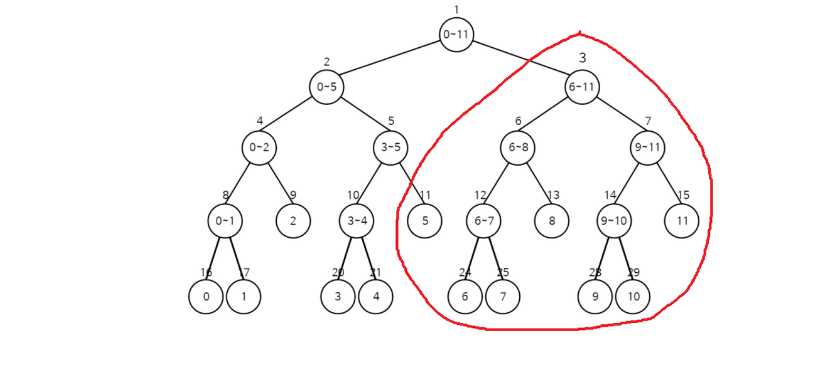
- 5~11은 0 ~ 11 에 포함되지만, 0 ~ 11 이 이 전체를 나타내지는 않기 때문에 분할하여 값을 찾는다.
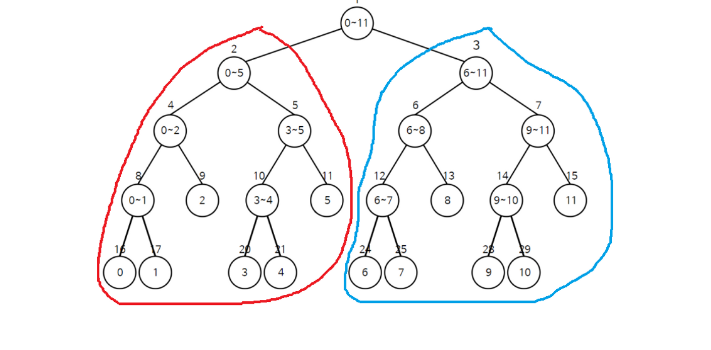
- 0 ~ 5 의 값에 5가 포함되지만, 마찬가지로 전체를 나타내지는 않기 때문에 분할한다.

- 0 ~ 2 는 값이 포함되지 않기 때문에 고려하지 않고 바로 0을 리턴한다.

- 3 ~ 5 의 값에 5가 포함되지만, 마찬가지로 전체를 나타내지는 않기 때문에 분할한다.
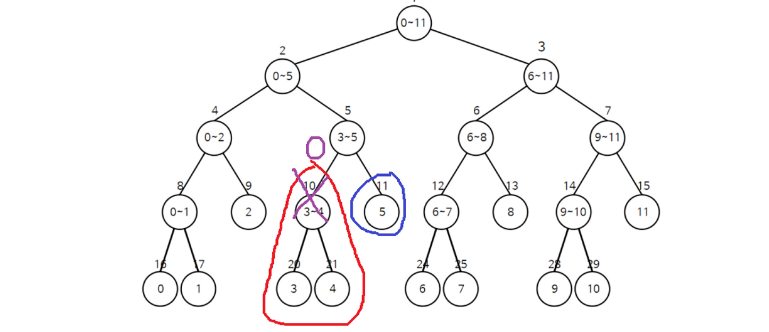
이때, 3 ~ 4 는 0 리턴, 5를 찾았으므로 5에 해당하는 값 (5) 리턴
- 이때 6 ~ 11 은 이 모든 값이 포함되므로 분할하지 않고 바로 값을 리턴하면된다

이를 위한 소스코드
/*
* start : 배열의 인덱스 시작지점
* end : 배열의 인덱스 종료지점
* index : tree 에 저장될 인덱스
* left : 찾고자 하는 합의 좌측 바운더리
* right : 찾고자 하는 합의 우측 바운더리
*/
sumTree(1, num.length, 1, 6, 12)
long sumTree(int start, int end, int index, int left, int right) {
//범위 바깥은 더할 필요없음
if(end < left || right < start) return 0;
//내가 찾는 범위의 안쪽이라면 바로 리턴
if(left <= start && end <= right) return tree[index];
//범위에 결쳐있어서 안쪽의 값이 필요하기 때문에 내부로 들어감
int mid = (start+end)/2;
return sumTree(start, mid, index*2, left, `) + sumTree(mid+1 , end, index*2+1, left, right);
}값의 수정
세그먼트 트리로 구성된 값은 수정이 용이하다.
수정에 영향을 받는 부분을 따라서 수정하면 되기 때문이다.
다음은 위의 예제에서 7번에 해당하는 값을 변경했을 때 전체 트리의 값을 변경하는 예제이다.
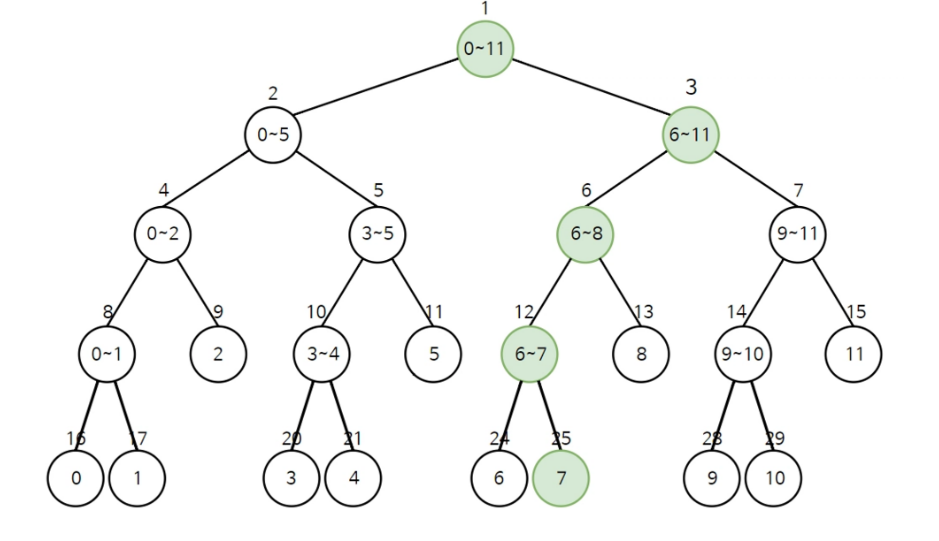
구간합을 구하는 방식과 유사하지만, 원하는 값이 포함되어 있다면 수정 연산을 진행하면서 탐색을 진행하면 된다.
/*
* start : 배열의 인덱스 시작지점
* end : 배열의 인덱스 종료지점
* index : 현재 참조하는 tree 인덱스
* targetIdx: 변경을 원하는 배열 인덱스
* changeNum: 변경할 숫자
*/
7번 인덱스의 수를 X로 변경!
update(1, 12, 1, 7, X)
void updateTree(int start, int end, int index, int targetIdx, long changeNum) {
//변경하는 익덱스가 범위에 없으면 변경하지 않고 리턴
if(targetIdx < start || end < targetIdx) return;
//범위에 해당하는 값이면 영향을 받으므로 그 만큼 기존 값을 빼고 새로운 값을 더함
tree[index] = tree[index] - num[targetIdx] + changeNum;
//원하는 end point에 도달하면 리턴
if(start == end) {
num[targetIdx] = changeNum;
return;
}
//세부 범위를 찾기 위해 탐색
int mid = (start + end )/2;
updateTree(start, mid, index*2, targetIdx, changeNum);
updateTree(mid+1, end, index*2+1, targetIdx, changeNum);
}
'JAVA > Algo 개념' 카테고리의 다른 글
| KMP -JAVA (0) | 2023.08.05 |
|---|---|
| 양방향 연결리스트 구현하기 (0) | 2023.08.05 |
| 슬라이딩 윈도우와 투 포인터 (0) | 2023.07.30 |
| TreeMap - Red-Black Tree (0) | 2023.07.26 |
| DP - LIS(최장 증가 수열) 및 0-1 Knapsack 개념 (JAVA) (1) | 2023.07.16 |

